
最初对声音概念的定义是以人的耳朵为标准的,空气的振动通过耳朵转化成生物电信号并传递给大脑,我们就听到了声音。人耳只对一定频率范围的声波敏感,超出这个范围的声波被定义为次声波和超声波,其实所有声波都是同种性质的波。声波在固体中可以表现为纵波也可以表现为横波,在流体中则只以纵波传递。这是因为传递横波需要剪切力的参与,而流体中的剪切力很小,不足以维持横波。我们的耳朵处于空气中,所以一般听到的都是在空气中传播的声音。空气中的声波是在声源激励下产生的一系列纵向压缩和膨胀交互的波动。在微观上看声波是靠分子热运动传递的,在宏观上看声波是靠空气的弹性传递的。
在空气中传播的声波是压缩和膨胀交替的压力脉动,或者叫压力波。人的耳朵能感受到的是振动,如果压力是一直上升或者一直下降的,人是听不到声音的。如图2所示的直管道,左侧活塞振动频率够快时,在右侧可以听到声音。如果活塞以比声音还快的速度突然向右动一下,则会发出一道激波,人会听到很响的一声。如果活塞以比声音还快的速度突然向左动一下,则会发出一道膨胀波,这个膨胀波在向右传播过程中会散开,到人的耳朵时不像压缩波那么强。激波是一种强扰动波,体现为压力的阶跃,其传播速度比声音的的速度大,一般较弱的压力扰动传播的速度,不论其频率如何,速度都一样,即声速。所以,流体中的声速不但代表了声音的传播速度,还代表了流体中局部压力变化传播的速度。
一般的流动中,影响流体速度的力有重力、压力和摩擦力三种。对于气体来说,重力经常可以忽略,且摩擦力比正压力小得多,所以流速变化主要受压力变化的影响。显然,某处压力的变化会以多快的速度传递到另一处,是流动问题中的关键问题。不考虑超声速情况,一般流动中这个压力传播速度就是声速。下面我们就来推导声速的关系式。
某处的发生变化后,如果是在开放的空间,则扰动以球面向四外传播,简化的问题中,可以研究压力扰动沿一维管道的传播。图3表示了几种理想化的简单压力波,显然(e)和(f)是最简单的理想化形式,表示压力的跃升和突降。现在取(e)来研究,这种压力扰动称为一道压缩波,当这个压力跃升很小时,称为微弱压缩波。
如图4左图所示,假设有一道弱压缩波在直管中以速度𝒄向右传播,未受扰动的气体是静止的,压力、密度和温度分别为𝒑𝟏,𝝆𝟏和𝑻𝟏,压缩波扫过后,气体具有了向右的一个速度𝛅𝒖,且压力、密度和温度变为𝒑𝟐,𝝆𝟐和𝑻𝟐
上面描述的是一种非定常流动,不好分析。如果我们取一个控制体随压缩波一起向右运动,就可以得到图4右图所示的定常流动,这样就可以用简单的一维定常关系式来分析了。这时,波的右侧气体速度变为𝒄,方向向左,左侧的气体速度变为𝒄-𝛅𝒖,方向也向左。
针对图4右图的坐标系和控制体列出连续方程和动量方程如下
整理后得
从上面两个关系式中消去𝛅𝒖,整理,就可以得到波速𝒄的表达式
对于声波这类微弱扰动,气体密度的变化非常小,\({{{\rho }_{2}}}/{{{\rho }_{1}}}\approx 1\),所以上式可以写为
对于未弱扰动,从状态1到状态2的变化非常小,让式(2)中的状态2趋向于状态1,就可以得到微分形式的表达式
这个关系式最早是由牛顿推导出来的,但在当时,对于气体的性质认识还不够深入,并不清楚压力随密度的变化管事是什么。牛顿使用了波义耳定律,即等温关系式来计算空气中的声速,得到的结果与测量值相比误差较大。1802年,拉普拉斯指出,声音的传播过程中伴随着气体的轻微压缩的膨胀,温度会有变化,并不是一个等温过程,而是一个绝热过程。1823年,拉普拉斯采用当时空气热特性的测量数据,计算出声速为337.15 m/s,与当时的测量值340.89 m/s 非常接近,因此拉普拉斯是公认的第一个正确推导出声速的科学家。
对于绝热过程,压力与密度的关系为
于是,压力随温度的变化关系式为
其中的𝑹是气体常数,对于空气,𝑹=287.06 J/(kg·K),因此空气中的声速关系式为
绝热指数在常温下基本是常数,𝜸=1.4,所以声速只与温度有关,而气体的温度就是分子平均热运动速度的表征,可见声速直接由分子热运动速度决定。
声速代表了压力变化在气体中传播的速度,是一个宏观速度,不过气体中压力信息的传递也是靠分子的微观热运动实现的,在“气体分子的速度”部分,我们已经给出了声速和分子速度的关系,这里再把它写出来如下
即声速比分子速度的均方根小一点。
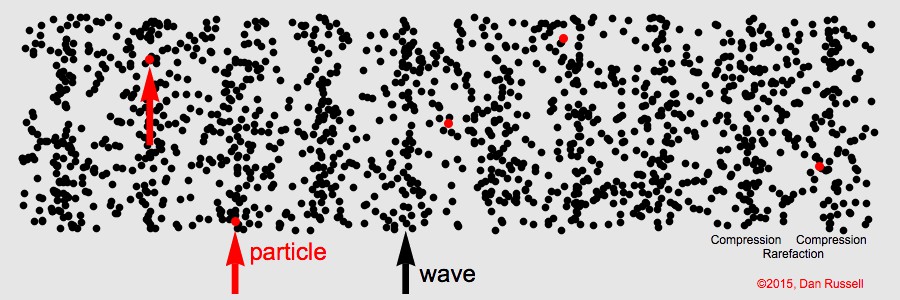
既然声速这种小扰动的传播过程是绝热过程,那么局部气体的温度就是有变化的,虽然非常微小。图5显示了声波传播过程中,空气局部的压缩和膨胀,压缩区的温度高一点,膨胀区的温度低一点。根据式(4)的声速公式,温度高的地方波速快一点,温度低的地方波速慢一点。也就是说声波内部不同的地方的局部波速并不相同,这也是纵波的特点,因为纵波的介质是沿传播方向振动的,振动速度叠加在整体波速上,必然导致局部波速的不同,整体传播的波速是压缩区和膨胀区波速的平均,如图6所示。

从式(1)到式(2)的过程中,我们加入了一个条件,就是扰动产生的气体参数变化很微小,如果是激波这样的强扰动,激波两侧的气流参数有突变的话,显然就不能得到式(2)了。实际上激波的波速也可以用类似的方法推导,详见“激波与膨胀波”部分。推导得出的激波波速比弱扰动波速大。
亚声速流动和超声速流动之所以有很大差异,根本原因就在于气体对于扰动是否来得及反应。气体的运动当然是符合牛顿定律的,流速是否会改变取决于受力,多数流动情况下(忽略重力和黏性力)这个力就是压力。局部的压力变化能以多快的速度传递,就代表了气体的反应速度。未弱扰动的传播速度是声速,强扰动的传播速度是激波的速度。一般我们听到的声音都是弱扰动,流动中通道收缩或转弯引起的局部压力变化的传递速度也是声速。而像炸弹爆炸和雷声这类情况则瞬间在局部产生较强的压力变化,其声音的传播速度在初始阶段是大于声速的。